Matrix Multiplication
We study the classic problem, 2D matrix multiplication. We will start with a short introduction about the problem and then discuss how to solve it parallel CPUs.
Problem Formulation
We are multiplying two matrices, A (MxK) and B (KxN). The numbers of columns of A must match the number of rows of B. The output matrix C has the shape of (MxN) where M is the rows of A and N the columns of B. The following example multiplies a 3x3 matrix with a 3x2 matrix to derive a 3x2 matrix.
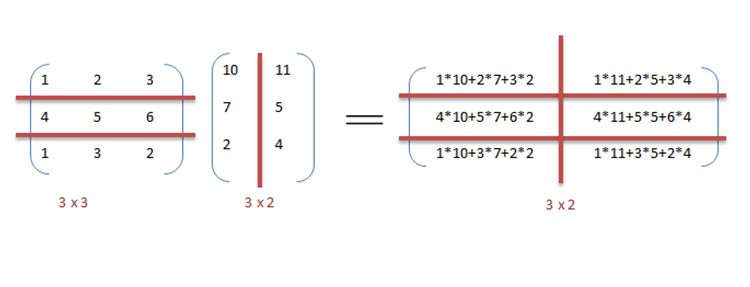
As a general view, for each element of C we iterate a complete row of A and a complete column of B, multiplying each element and summing them.
We can implement matrix multiplication using three nested loops.
for(int m=0; m<M; m++) { for(int n=0; n<N; n++) { C[m][n] = 0; for(int k=0; k<K; k++) { C[m][n] += A[m][k] * B[k][n]; } } }
Parallel Patterns
At a fine-grained level, computing each element of C is independent of each other. Similarly, computing each row of C or each column of C is also independent of one another. With task parallelism, we prefer coarse-grained model to have each task perform rather large computation to amortize the overhead of creating and scheduling tasks. In this case, we avoid intensive tasks each working on only a single element. by creating a task per row of C to multiply a row of A by every column of B.
// C = A * B // A is a MxK matrix, B is a KxN matrix, and C is a MxN matrix void matrix_multiplication(int** A, int** B, int** C, int M, int K, int N) { tf::Taskflow taskflow; tf::Executor executor; for(int m=0; m<M; ++m) { taskflow.emplace([m, &] () { for(int n=0; n<N; n++) { for(int k=0; k<K; k++) { C[m][n] += A[m][k] * B[k][n]; // inner product } } }); } executor.run(taskflow).wait(); }
Instead of creating tasks one-by-one over a loop, you can leverage Taskflow::
// perform parallel iterations on the range [0, M) with the step size of 1 tf::Task task = taskflow.for_each_index(0, M, 1, [&] (int m) { for(int n=0; n<N; n++) { for(int k=0; k<K; k++) { C[m][n] += A[m][k] * B[k][n]; } } });
Please visit Parallel Iterations for more details.
Benchmarking
Based on the discussion above, we compare the runtime of computing various matrix sizes of A, B, and C between a sequential CPU and parallel CPUs on a machine of 12 Intel i7-8700 CPUs at 3.2 GHz.
| A | B | C | CPU Sequential | CPU Parallel |
|---|---|---|---|---|
| 10x10 | 10x10 | 10x10 | 0.142 ms | 0.414 ms |
| 100x100 | 100x100 | 100x100 | 1.641 ms | 0.733 ms |
| 1000x1000 | 1000x1000 | 1000x1000 | 1532 ms | 504 ms |
| 2000x2000 | 2000x2000 | 2000x2000 | 25688 ms | 4387 ms |
| 3000x3000 | 3000x3000 | 3000x3000 | 104838 ms | 16170 ms |
| 4000x4000 | 4000x4000 | 4000x4000 | 250133 ms | 39646 ms |
The speed-up of parallel execution becomes clean as we increase the problem size. For example, at 4000x4000, the parallel runtime is 6.3 times faster than the sequential runtime.